Anisotropies

We have already seen that the observed variability of a phenomenon is most often due to many causes ranging over various scales. Consider a nested model $/gamma({/boma h})$ consisting of the sum of a micro-structure $/gamma_1({/boma h})$ and a macro-structure $/gamma_2({/boma h})$:

There is no reason for these two-component structures to have the same directions of anisotropy. Thus, the micro-structure $/gamma_1$, characterizing, for example, the measurement errors and the phenomena of diffusion and concretion at very small distances, may be isotropic, while the macro-structure $/gamma_2$, characterizing, for example, the lenticular deposits of the mineralization, may reveal directions of preferential alignment of these lenses. 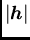In such an example, the structure $/gamma_1$ depends only on the modulus $/vert{/boma h}/vert$ of the vector ${/boma h}$ and it can be represented by any one of the isotropic models presented in Section 4.3. 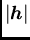On the other hand, the macro-structure $/gamma_2$ will require a model $/gamma_2(/vert{/boma h}/vert,/alpha,/varphi)$ which depends not only on the modulus $/vert{/boma h}/vert$ but also on the direction of the vector ${/boma h}$.

Anisotropies will be represented by the method of reducing them to the isotropic case either by a linear transformation of the rectangular coordinates $/gamma(h_u, h_v, h_w)$ of the vector ${/boma h}$ in the case of geometric anisotropy, or by representing separately each of the directional variabilities concerned in the case of zonal anisotropy.