



Next: Proportional Effect
Up: Anisotropies
Previous: Remark
Contents
Let  and
and 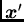 be two points with coordinates
be two points with coordinates
 and
and
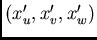 .
Without any hypothesis of stationarity,
.
Without any hypothesis of stationarity,
- (i)
- the expectation of the random function
 depends on the
position
depends on the
position  , i.e., on the
three coordinates
, i.e., on the
three coordinates
 ;
;
- (ii)
- the semi-variogram
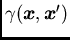 or the covariance
or the covariance
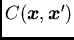 depends on
the two locations
depends on
the two locations  and
and 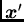 of the random variables
of the random variables
 and
and 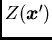 , i.e., on the six
coordinates
, i.e., on the six
coordinates
 and
and
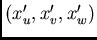 ,
,
It was indicated that a hypothesis of quasi-stationarity
is generally sufficient for geostatistical applications. This hypothesis
amounts to assuming that:
- (i)
- the expectation is quasi-constant over limited neighborhoods and,
thus,
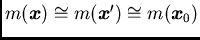 when the two points
when the two points
 and
and 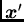 are inside
the neighborhood
are inside
the neighborhood
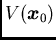 centered on the point
centered on the point 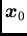 ;
;
- (ii)
- inside such a neighborhood
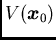 , the structural functions
, the structural functions
 or
or  depend only on the vector of the separating distance
depend only on the vector of the separating distance
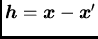 and
not on the two locations
and
not on the two locations  and
and 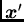 ; however, this structural function
depends on the particular neighborhood
; however, this structural function
depends on the particular neighborhood
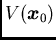 , i.e., on the point
, i.e., on the point 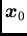 ,
,
The construction of a model of quasi-stationarity thus amounts to building a
model of the structural function
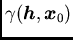 which depends on the
argument
which depends on the
argument 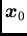 .
.




Next: Proportional Effect
Up: Anisotropies
Previous: Remark
Contents
Rudolf Dutter
2003-03-13
![]() and
and ![]() be two points with coordinates
be two points with coordinates
![]() and
and
![]() .
Without any hypothesis of stationarity,
.
Without any hypothesis of stationarity,
![]() which depends on the
argument
which depends on the
argument ![]() .
.