



Next: Correction of Geometric Anisotropy
Up: Anisotropies
Previous: Anisotropies
Contents
A semi-variogram
 or a covariance
or a covariance
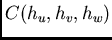 has a
geometric anisotropy when the anisotropy can be reduced to isotropy by a
mere linear transformation of the coordinates:
has a
geometric anisotropy when the anisotropy can be reduced to isotropy by a
mere linear transformation of the coordinates:
with
or, in matrix form,
where 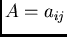 represents the matrix of transformation of the coordinates,
and
represents the matrix of transformation of the coordinates,
and  and
and 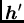 are column-vectors of the coordinates.
are column-vectors of the coordinates.
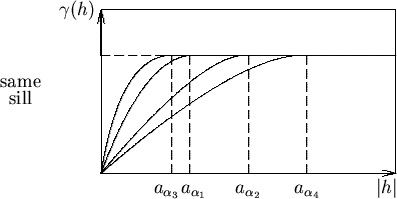
An example is given in Figure 4.6, which shows four semi-variograms
for four horizontal directions
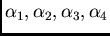 .
Spherical models with identical
sills and ranges of
.
Spherical models with identical
sills and ranges of
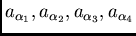 have been fitted to these semi-variograms. The directional graph of the ranges,
i.e., the variation of the ranges
have been fitted to these semi-variograms. The directional graph of the ranges,
i.e., the variation of the ranges 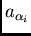 as a function of the direction
as a function of the direction 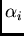 ,
is also shown in Figure 4.5. There are three possible cases.
,
is also shown in Figure 4.5. There are three possible cases.
Figure 4.5:
Ranges in Case of Anisotropy.
![/begin{figure}/begin{center}
/mbox
{/beginpicture
/setcoordinatesystem units <1c...
...5
/put {$a_{/alpha_{4}}$} [b] at -1.3 0.75
/endpicture}
/end{center}/end{figure}](img485.png) |
Figure 4.6:
Geometric Anisotropy.
 |
- (i)
- The graph can be approximated to a circle of radius
 , i.e.,
, i.e.,
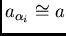 ,
for all horizontal directions
,
for all horizontal directions 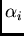 and the phenomenon can thus be
considered as isotropic and characterized by a spherical model of
range
and the phenomenon can thus be
considered as isotropic and characterized by a spherical model of
range  .
.
- (ii)
- The graph can be approximated by an ellipse, i.e., by a shape which
is a linear transform of a circle. By applying this linear transformation
to the coordinates of vector
 , the isotropic case is produced
(circular graph).
The phenomenon is a geometric anisotropy.
, the isotropic case is produced
(circular graph).
The phenomenon is a geometric anisotropy.
- (iii)
- The graph cannot be fitted to a second-degree curve and the second
type of anisotropy must be considered, i.e., zonal anisotropy in
certain directions,
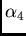 , for example, on Figure 4.5.
, for example, on Figure 4.5.
If, instead of transition structures of range 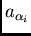 as in Figure 4.5,
the directional semi-variograms are of the linear type,
as in Figure 4.5,
the directional semi-variograms are of the linear type,
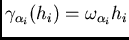 , then the
directional graphs of the inverses of the slopes at the origin
, then the
directional graphs of the inverses of the slopes at the origin
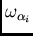 will be
considered. A hypothesis of isotropy, geometric anisotropy or zonal
anisotropy will then be adopted according to whether or not this directional
graph can be fitted to a circle or an ellipse.
will be
considered. A hypothesis of isotropy, geometric anisotropy or zonal
anisotropy will then be adopted according to whether or not this directional
graph can be fitted to a circle or an ellipse.




Next: Correction of Geometric Anisotropy
Up: Anisotropies
Previous: Anisotropies
Contents
Rudolf Dutter
2003-03-13
![]() or a covariance
or a covariance
![]() has a
geometric anisotropy when the anisotropy can be reduced to isotropy by a
mere linear transformation of the coordinates:
has a
geometric anisotropy when the anisotropy can be reduced to isotropy by a
mere linear transformation of the coordinates:
![]() .
Spherical models with identical
sills and ranges of
.
Spherical models with identical
sills and ranges of
![]() have been fitted to these semi-variograms. The directional graph of the ranges,
i.e., the variation of the ranges
have been fitted to these semi-variograms. The directional graph of the ranges,
i.e., the variation of the ranges ![]() as a function of the direction
as a function of the direction ![]() ,
is also shown in Figure 4.5. There are three possible cases.
,
is also shown in Figure 4.5. There are three possible cases.
![]() as in Figure 4.5,
the directional semi-variograms are of the linear type,
as in Figure 4.5,
the directional semi-variograms are of the linear type,
![]() , then the
directional graphs of the inverses of the slopes at the origin
, then the
directional graphs of the inverses of the slopes at the origin
![]() will be
considered. A hypothesis of isotropy, geometric anisotropy or zonal
anisotropy will then be adopted according to whether or not this directional
graph can be fitted to a circle or an ellipse.
will be
considered. A hypothesis of isotropy, geometric anisotropy or zonal
anisotropy will then be adopted according to whether or not this directional
graph can be fitted to a circle or an ellipse.