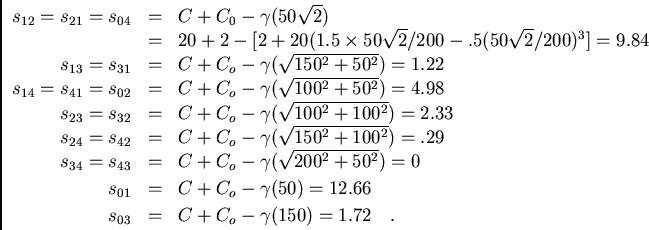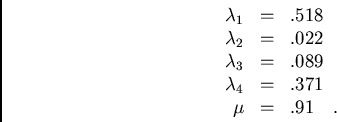Next: Block Kriging
Up: Estimation of Resources
Previous: Discussion
Contents
Point Kriging
Suppose that instead of trying to estimate a block one simply wants to
estimate the grade at one particular point. Then all the coefficients of the
krige system become
very simple and involve only some distance computation. The matrix remains
the same as before, it depends only on the samples at locations  .
.
Let us take an example:
Example
6.1: (David, 1977[5])
Consider a stratiform deposit with a spherical variogram where 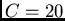 ;
;
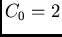 ;
; 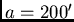 and one wants to estimate the grade
and one wants to estimate the grade 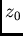 of point
of point
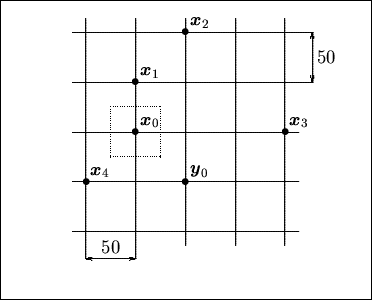
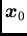 (Figure 6.2)
from points
(Figure 6.2)
from points
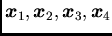 ,
where the grades are
,
where the grades are
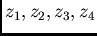 . How do
we weight these known grades for the estimation?
. How do
we weight these known grades for the estimation?
Figure 6.2:
Point Kriging: Sketch of Sample Locations.
 |
The definition of the variogram can now be given by the formula
and
Because the regions of the known values  and also the region
and also the region
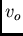 of the interesting value are at a point support, we denote
of the interesting value are at a point support, we denote
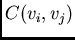
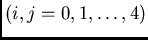 simply
simply 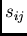 , such that we
obtain the following kriging system:
, such that we
obtain the following kriging system:
We thus only need the values of the covariances 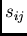 . The diagonal
elements of the matrix are all equal the variances, i.e.
. The diagonal
elements of the matrix are all equal the variances, i.e.
Furthermore, from the sketch of the sampling plan, it can be seen that
From this the solution of the system of equations follows:
- Remark 1:
- Although samples
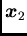 and
and 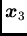 have altogether
little influence on the overall estimation, their relative influence
is not linear in relation to their distance from
have altogether
little influence on the overall estimation, their relative influence
is not linear in relation to their distance from 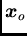 . Sample
. Sample 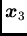 is further away than
is further away than 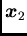 and carries more
influence (8.9%) than sample
and carries more
influence (8.9%) than sample 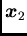 . This is due to the fact that
. This is due to the fact that
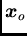 is directly under the influence of
is directly under the influence of 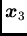 , while
, while 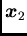 is in fact in the ``shadow'' of
is in fact in the ``shadow'' of 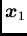 . This
means that introducing the covariances in the computation of weights will
not give undue weight to clusters of samples as a simple distance method
would do.
. This
means that introducing the covariances in the computation of weights will
not give undue weight to clusters of samples as a simple distance method
would do.
- Remark 2:
- Suppose that we now want to estimate the point
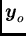 from
from
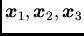 and
and 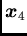 . The only new
effort is to recompute the
. The only new
effort is to recompute the  , since the matrix
, since the matrix
 remains unchanged. This should be kept in mind when writing
a program of kriging since it saves a lot of computing time.
remains unchanged. This should be kept in mind when writing
a program of kriging since it saves a lot of computing time.




Next: Block Kriging
Up: Estimation of Resources
Previous: Discussion
Contents
Rudolf Dutter
2003-03-13
![]() .
.
![]() ;
;
![]() ;
; ![]() and one wants to estimate the grade
and one wants to estimate the grade ![]() of point
of point
![]() (Figure 6.2)
from points
(Figure 6.2)
from points
![]() ,
where the grades are
,
where the grades are
![]() . How do
we weight these known grades for the estimation?
. How do
we weight these known grades for the estimation?
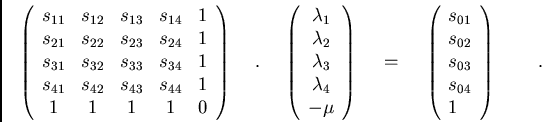
![]() . The diagonal
elements of the matrix are all equal the variances, i.e.
. The diagonal
elements of the matrix are all equal the variances, i.e.