This condition for the existence and the uniqueness of the solution of the kriging system thus entails that the kriging variance is non-negative.
- (i)
- an estimator
 identical to the known grade
identical to the known grade  , of the support
, of the support
 ;
;
- (ii)
- a zero kriging variance,
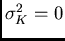 .
.
- (i)
- whatever the supports
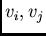 of the data and the support
of the data and the support  to be
estimated, some data supports may partially overlap,
to be
estimated, some data supports may partially overlap,
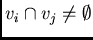 , but for
, but for  it is imperative that
it is imperative that
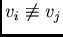 -some
data supports may be included in the volume
-some
data supports may be included in the volume  to be estimated,
to be estimated,  ;
;
- (ii)
- whatever the underlying structure characterized by the model
 or
or
 , the structure may be isotropic
or anisotropic, nested or not.
, the structure may be isotropic
or anisotropic, nested or not.
In cartography, it is said that ``the kriged surface passes through the experimental points''. Not every estimation procedure has this property, especially procedures using least square polynomials.
Thus, two identical data configurations would provide the same kriging
matrix ![]() and it is then enough to take the inverse matrix
and it is then enough to take the inverse matrix ![]() only once.
The two solution column vectors
only once.
The two solution column vectors
![]() and
and
![]() are then obtained by taking
the products of the one inverse matrix
are then obtained by taking
the products of the one inverse matrix ![]() and the respective
second-member vectors:
and the respective
second-member vectors:
This, of course, suggests the very systematic and regular proceeding in data collecting.
- (i)
- The geometry of the domain
 to be estimated, expressed in the
term
to be estimated, expressed in the
term
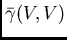 in the expression of the kriging variance
in the expression of the kriging variance
 .
.
- (ii)
- The distances between
 and the supports
and the supports  of the information,
expressed by the terms
of the information,
expressed by the terms
 of the vector
of the vector  .
.
- (iii)
- The geometry of the data configuration as expressed by the terms
 of the kriging matrix
of the kriging matrix  . The accuracy of an estimation
depends not only on the number of data but also on their configuration
in relation with the main features of the regionalization as
characterized by the structural function
. The accuracy of an estimation
depends not only on the number of data but also on their configuration
in relation with the main features of the regionalization as
characterized by the structural function
 in the various terms
in the various terms
 .
.
- (iv)
- The main structural features of the variability of the phenomenon
under study as characterized by the semi-variogram model
 .
.
Consider the estimation in two dimensions of the panel ![]() by the symmetric
configuration of the four data points
by the symmetric
configuration of the four data points ![]() as shown on Figure
6.1. The
underlying mineralization shows a preferential direction
as shown on Figure
6.1. The
underlying mineralization shows a preferential direction ![]() of continuity
which appears in the anisotropic semi-variogram
of continuity
which appears in the anisotropic semi-variogram
![]() as a slower
variability in the direction
as a slower
variability in the direction ![]() . The kriging system thus gives a greater weight
to the data
. The kriging system thus gives a greater weight
to the data ![]() and
and ![]() , although they are at the same distance from
, although they are at the same distance from ![]() as
as
![]() and
and ![]() .
.
![/begin{figure}/begin{center}
/mbox
{/beginpicture
/setcoordinatesystem units <1c...
... [t] at 6.225 3.1
/put {$V$} at 3.8 3.35
}
/endpicture}
/end{center}/end{figure}](img955.png)