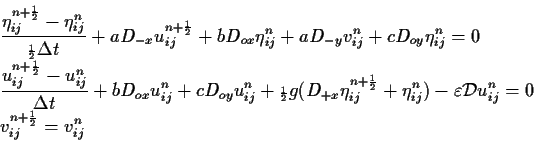 |
(7.34) |
Neglecting external forces in the two dimensional shallow waters system, (3.2-3.4), and freezing coefficients the finite differences scheme is written as (4.38) for the row-wise j sweep.
With coefficient approximation:
![]() ,
,
![]() ,
,
![]() .
.
For the column-wise i sweep we get:
We can make the Fourier expansion again using:
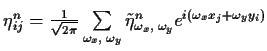 |
(7.35) | ||
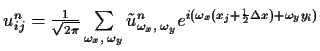 |
(7.36) | ||
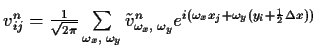 |
(7.37) | ||
| (7.38) |
The implicit model is formulated, employing matrix notation, by:
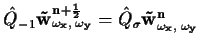 expanded in (4.43) and
expanded in (4.43) and
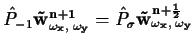 expanded in (4.44).
expanded in (4.44).
In this case we study stability by examining the spectral radius of
the amplification matrices:
![]() and
and
![]() .
They should not be greater than one:
.
They should not be greater than one:
![]() and
and
![]() for all
for all ![]() in
in ![]() .
.
Again, the system is stable for practical values of ![]() and
and ![]() without heavy dependence on the maximum depth a and velocities band c. For a practical value of
without heavy dependence on the maximum depth a and velocities band c. For a practical value of
![]() the allowed time
step is shown in figure 4.3. For
the allowed time
step is shown in figure 4.3. For
![]() it is required that
it is required that
![]() .
The 12-hour period
astronomic wave should be modeled employing a time step with at least
15 grid points per wave length. In every case we must choose time
steps smaller than 45 minutes, in agreement with our previous result
for the explicit model.
.
The 12-hour period
astronomic wave should be modeled employing a time step with at least
15 grid points per wave length. In every case we must choose time
steps smaller than 45 minutes, in agreement with our previous result
for the explicit model.
The Río de la Plata wind storm tide simulation requires a
![]() rather big, as high as 1000, due to the large depth and
steep variations in the sea bottom. In that case, the time step must
be selected below 5 minutes due to the stability requirements.
rather big, as high as 1000, due to the large depth and
steep variations in the sea bottom. In that case, the time step must
be selected below 5 minutes due to the stability requirements.