Linear Behavior at the Origin

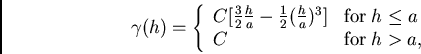
This is the most frequent type of behavior encountered in mining practice (variogram of grades and accumulations) and it is most often accompanied by a nugget effect.

(a)

Spherical model:

(b)

Exponential model:

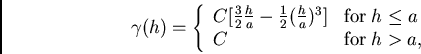
Note that the spherical model effectively reaches its sill for a finite distance $r = a =$ range, while the exponential model reaches its sill only asymptotically, cf. Figure 4.15. However, because of experimental fluctuations of the variogram, no distinction will be made in practice between an effective and an asymptotic sill. For the exponential model, the practical range $a'$ can be used with $a'=3a$, for which $/gamma(a')=C(1 - e^{-3})=.95C$

Figure 4.15: Variogram Models.

The difference between the spherical and exponential models is the distance (abscissa) at which their tangents at the origin intersect the sill, cf. Figure 4.15:

$r = 2a/3$, two-third of the range for the spherical model;

$r = a = a'/3$, one third of the practical range for the exponential model.
Thus, the spherical model reaches its sill faster than the exponential model.