



Next: Higher Moments
Up: Characteristic Parameters of a
Previous: Quantiles and Percentiles
Contents
Measures of Dispersion
The location parameter by its own, usually does not give a picture of the
distribution (only the location!). Another characteristic parameter of
the distribution should give the variation of the values around the
location parameter. We could use a function of deviations from the
mean
However, how it is easily seen, the sum and also the mean of these
deviations are zero. Therefore the square of the deviations is
frequently used, and the mean of these squares of deviations
is called variance. The standard deviation or simply
deviation is defined by
For quick computation of 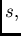 the formula
the formula
may be used.
If we have a classification of the data in 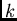 groups with
groups with
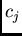 as mean of the
as mean of the 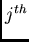 class and
class and 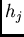 as frequency, the
approximate identity is
as frequency, the
approximate identity is
Remark: If we denote the random variable by  , from which the values
, from which the values
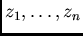 have been realized, then the variance of the
variable can be computed from all possible values by
have been realized, then the variance of the
variable can be computed from all possible values by
where 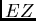 is defined as in Subsection 2.2.1 by
is defined as in Subsection 2.2.1 by
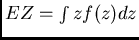 .
.
The coefficient of variation is defined by
which is the relation of the deviation (variability of the data) to
the mean. 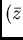 should, of course, be greater than zero.)
should, of course, be greater than zero.)
Linear Transformations: Are the data values transformed by
using two constants  and
and 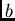 , then the mean of
, then the mean of 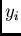 is obtained
by
is obtained
by
and the variance is
respectively the standard deviation is
Find out the arithmetic mean and the standard deviation of the
standardized quantities
Other Measures of Dispersion: The interquartile range
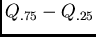 approximates the standard deviation (if the
assumption of the approximate normal distribution can be used) by
approximates the standard deviation (if the
assumption of the approximate normal distribution can be used) by
the median of absolute deviations from the median
(Medmed) by
It may easily be seen, that these two measures of dispersion are much
more stable (resistant) in respect of changes in the data than the usual
(previously defined) deviation, and are, therefore, much more
recommendable for the practice.




Next: Higher Moments
Up: Characteristic Parameters of a
Previous: Quantiles and Percentiles
Contents
Rudolf Dutter
2003-03-13
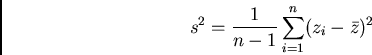
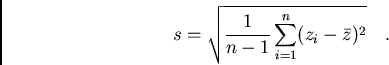
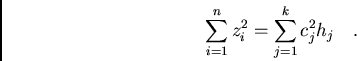
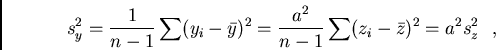
![]() approximates the standard deviation (if the
assumption of the approximate normal distribution can be used) by
approximates the standard deviation (if the
assumption of the approximate normal distribution can be used) by