Location Parameters

The location of a distribution of a statistical variable can usually be presented by a single number. Mostly the arithmetic mean is used. Suppose, we have $n$ measurements ($n$ numbers denoted by $z_{i}, i=1,/ldots,n,$), e.g. values of grades of copper. Then the arithmetic mean is

If we imagine some weights at each points then it represents the center of gravity.

In case of classified data (as in a histogram) we can find $/bar{z}$ faster via the frequencies. Denote the mean value of a class ((max-min)/2) by $c_{j}$, the corresponding absolute frequency by $h_{j}$ and the relative frequency by $f_{j}$. If there are $k$ classes then $/bar{z}$ is approximately

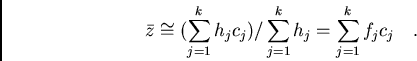
Because the arithmetic mean is equivalent to the center of gravity of the distribution, it is also very sensitive to outliers, values which are very far from the mass of data (gross errors). A more realistic location parameter, which represents the ``center'' of the distribution, is the median. We denote it by $/tilde{z}$, and it is a value which splits the data set into two equal parts: At most 50% of the values are smaller and at most 50% are larger. In frequency tables and in stem and leaf displays, $/tilde{z}$ is simply found by counting or by taking the value with the highest depth, in cumulative frequency polygons at the $x$-value where the $y$-value reaches 50%.

Other location parameters are the mode (the most probable value), the mean of the range, etc.

Remark: If we interpret a statistical variable $Z$ as a random variable, which is-as mentioned in Chapter 1-a mapping of elementary events at (a subset of) real numbers, we name the (weighted) mean of all possible values (mathematical) expectation $E$ and define it formally with the help of the density function $f$ (ev. relative frequency) by