Next: Some Typical Problems and
Up: The Geostatistical Language
Previous: Case Study, After J.P.
Contents
Suppose there is a deposit 
, which is divided by 
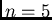blocks 
to 
. The true (averaged) values 
of 
in 
and the estimated ones 
are given in Table
1.1.
Table 1.1:
Values of a Fictive Deposit.
 |
|
 |
 |
 |
 |
 |
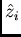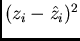| 1 |
5 |
6 |
0 |
1 |
-1 |
1 |
| 2 |
7 |
6 |
4 |
1 |
1 |
1 |
| 3 |
6 |
4 |
1 |
1 |
2 |
4 |
| 4 |
2 |
4 |
9 |
1 |
-2 |
4 |
| 5 |
5 |
5 |
0 |
0 |
0 |
0 |
 |
25 |
25 |
14 |
4 |
0 |
10 |
The mean value of 
obviously is
The variance of the spatial distribution is
and the variance of the estimated values
The estimation variance therefore is
Empirically we can see that the approximate relation between the three
variances is
In order to construct a tolerance interval for the true values of
we assume an approximate normal distribution of the associated random
variable. The approximate (95 %)
tolerance interval for then is
or, in detail,
Next: Some Typical Problems and
Up: The Geostatistical Language
Previous: Case Study, After J.P.
Contents
Rudolf Dutter
2003-03-13
