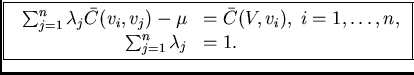Next: Matrix Form
Up: The Kriging Estimator
Previous: Non-bias Condition
Contents
Minimum Estimation Variance
The estimation variance
 can be expanded as follows:
can be expanded as follows:
with
The terms  are eliminated and, thus, we have
are eliminated and, thus, we have
The estimation variance can, thus, be expressed as a quadratic form in
 , and is to be minimized subject to the non-bias condition
, and is to be minimized subject to the non-bias condition
 .
The optimal weights are obtained from standard Lagrangian techniques by
setting to zero each of the
.
The optimal weights are obtained from standard Lagrangian techniques by
setting to zero each of the  partial derivatives (in respect to
partial derivatives (in respect to  and
to the Lagrange parameter
and
to the Lagrange parameter  ) of
) of
This procedure provides a system of  linear equations in
linear equations in
 unknowns (the
unknowns (the  weights
weights  , and the Lagrange parameter
, and the Lagrange parameter
 ) which is called the ``kriging system'':
) which is called the ``kriging system'':
The minimum estimation variance, or ``kriging variance'', can then be
written as
This kriging system can also be expressed in terms of the semi-variogram
function
 , particularly when the random function
, particularly when the random function  is intrinsic only and the covariance function
is intrinsic only and the covariance function  is not defined:
is not defined:




Next: Matrix Form
Up: The Kriging Estimator
Previous: Non-bias Condition
Contents
Rudolf Dutter
2003-03-13
![]() can be expanded as follows:
can be expanded as follows:



![]() , and is to be minimized subject to the non-bias condition
, and is to be minimized subject to the non-bias condition
![]() .
The optimal weights are obtained from standard Lagrangian techniques by
setting to zero each of the
.
The optimal weights are obtained from standard Lagrangian techniques by
setting to zero each of the ![]() partial derivatives (in respect to
partial derivatives (in respect to ![]() and
to the Lagrange parameter
and
to the Lagrange parameter ![]() ) of
) of