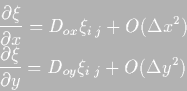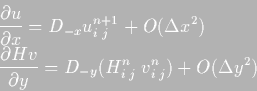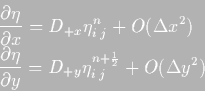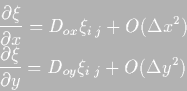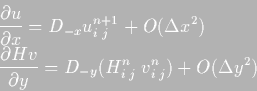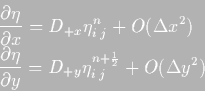Next: Grid refinement study, test
Up: Numerical model accuracy.
Previous: Numerical model accuracy.
Accuracy analytical determination.
To prove that the developed model is second order accurate we must
demonstrate that the numerical approximations to derivatives used in the
discrete form of the Shallow-water equations are all of second order.
The central operators defined in Section 4.2.3
are all of second order when applied in the difference scheme
(Hirsch, 1991):
- 1.
- Operators
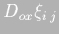 and
and
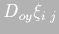 defined in
(4.10) are both centered in space, then:
defined in
(4.10) are both centered in space, then:
- 2.
- Operators
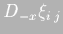 and
and
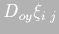 defined in
(4.11) are always centered in space. As an example,
when D-x and D-y are employed in (4.2),
they are centered in the middle of cell, where the level is
calculated, using data from the sides of the cell to make the
differentiation (see figure 4.1 for an explanation of the
staggered grid) and hence:
defined in
(4.11) are always centered in space. As an example,
when D-x and D-y are employed in (4.2),
they are centered in the middle of cell, where the level is
calculated, using data from the sides of the cell to make the
differentiation (see figure 4.1 for an explanation of the
staggered grid) and hence:
- 3.
- Similarly, operators
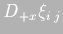 and
and
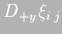 defined in (4.12) are centered in space.
As an example case: when they are used in equations
(4.3) and (4.7) respectively, they are
centered in the sides of the cell, employing data form adjacent cells
to make the differentiation, therefore:
defined in (4.12) are centered in space.
As an example case: when they are used in equations
(4.3) and (4.7) respectively, they are
centered in the sides of the cell, employing data form adjacent cells
to make the differentiation, therefore:
- 4.
- Approximations to the second derivative
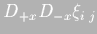 and
and
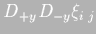 introduced in (4.13),
employed in the Laplacian (4.14), and hence in
(4.3) and (4.7) are second order
accurate. Therefore, the Laplacian is second order accurate.
introduced in (4.13),
employed in the Laplacian (4.14), and hence in
(4.3) and (4.7) are second order
accurate. Therefore, the Laplacian is second order accurate.
Since every finite difference operator being employed and boundary
conditions are second order accurate, the numerical scheme has the same
accuracy.




Next: Grid refinement study, test
Up: Numerical model accuracy.
Previous: Numerical model accuracy.
Elias Kaplan M.Sc.
1998-07-22