



Next: The Variogram
Up: The Geostatistical Language
Previous: Regionalized Variable and Random
Contents
Mean and Variance
A random function
 depends on two arguments, one is
for the elementary random events
depends on two arguments, one is
for the elementary random events  and the other one for the
geographical place
and the other one for the
geographical place  . In this subsection we only consider a
particular place
. In this subsection we only consider a
particular place  , such that
, such that 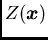 may be seen as a usual
random variable. An important tool for the description of the distribution
is the notion of the (mathematical)
expectation
may be seen as a usual
random variable. An important tool for the description of the distribution
is the notion of the (mathematical)
expectation 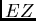 of the
random variable
of the
random variable  . It is defined by the weighted mean of all possible
values, weighted by the probability density
. It is defined by the weighted mean of all possible
values, weighted by the probability density  , namely
, namely
The integration is over the whole domain of values, e.g. in the case of
grades in % it would be from 0 to 100%. In case of only finite many possible
values 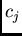 with corresponding probabilities
with corresponding probabilities
 we simply use the sum:
we simply use the sum:
This theoretical expectation of a random variable is often simply called
mean,  .
.
The variance  of a random variable is defined by the
expected value (i.e. the mean) of the quadratic deviation from the mean
of a random variable is defined by the
expected value (i.e. the mean) of the quadratic deviation from the mean  .
In the general case we have
.
In the general case we have
and in the case of finite many possible values
The square root of the variance is also called
standard deviation
or (sometimes) dispersion. It represents a measure
for the width of the distribution, i.e. for the variability of  . The unit
of the dispersion is of course the same as that of the variable
. The unit
of the dispersion is of course the same as that of the variable  , and we
may define e.g. a tolerance interval
, and we
may define e.g. a tolerance interval
 which says that a realization will fall
in this interval with a certain (high) probability.
which says that a realization will fall
in this interval with a certain (high) probability.
In practice, if  empirical measurements (realizations)
empirical measurements (realizations)
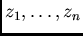 of a random variable are at hand,
the expectation may be estimated by the simple calculation of the mean.
For this estimated mean
of a random variable are at hand,
the expectation may be estimated by the simple calculation of the mean.
For this estimated mean  we have
we have
and for the estimated variance
where the denominator in general is  to compensate the loss of
information because of estimation of
to compensate the loss of
information because of estimation of  .
.




Next: The Variogram
Up: The Geostatistical Language
Previous: Regionalized Variable and Random
Contents
Rudolf Dutter
2003-03-13
![]() depends on two arguments, one is
for the elementary random events
depends on two arguments, one is
for the elementary random events ![]() and the other one for the
geographical place
and the other one for the
geographical place ![]() . In this subsection we only consider a
particular place
. In this subsection we only consider a
particular place ![]() , such that
, such that ![]() may be seen as a usual
random variable. An important tool for the description of the distribution
is the notion of the (mathematical)
expectation
may be seen as a usual
random variable. An important tool for the description of the distribution
is the notion of the (mathematical)
expectation ![]() of the
random variable
of the
random variable ![]() . It is defined by the weighted mean of all possible
values, weighted by the probability density
. It is defined by the weighted mean of all possible
values, weighted by the probability density ![]() , namely
, namely

![]() of a random variable is defined by the
expected value (i.e. the mean) of the quadratic deviation from the mean
of a random variable is defined by the
expected value (i.e. the mean) of the quadratic deviation from the mean ![]() .
In the general case we have
.
In the general case we have
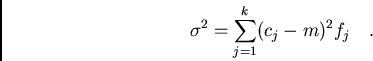
![]() empirical measurements (realizations)
empirical measurements (realizations)
![]() of a random variable are at hand,
the expectation may be estimated by the simple calculation of the mean.
For this estimated mean
of a random variable are at hand,
the expectation may be estimated by the simple calculation of the mean.
For this estimated mean ![]() we have
we have

