



Next: Fallstudie: Kohlelagerstätte
Up: Simulation of an Unconditional
Previous: The ``Turning Bands'' Method
Contents
Non-conditional Simulation in one Dimension
In some special cases (as with the spherical or the exponential model) it
is possible to express the one-dimensional covariances  in
the form of a convolution product of a function
in
the form of a convolution product of a function  and its transpose
and its transpose
 :
:
Therefore a random function in one dimension can sometimes be simulated
by using the method of moving average. This will be shortly illustrated
with the spherical model.
The covariance function is defined by
 is computed via the derivative
is computed via the derivative
which means,
This function may be written as convolution product of the function
with its transpose. We have, which is easily to be verified,
In practice we would proceed as follows: Generate at equidistant points

 with distance
with distance 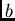 uniformly distributed
random numbers
uniformly distributed
random numbers
 in the interval
in the interval ![$[-a/2, a/2]$](img1160.png) .
The distance
.
The distance  should be at least
should be at least  . Then a realization of
. Then a realization of  (the one-dimensional random function) is produced through linear
combination (moving average)
(the one-dimensional random function) is produced through linear
combination (moving average)
where of course,  for
for  . Because of the
discretization (
. Because of the
discretization (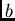 should not be too large) the distribution properties
of
should not be too large) the distribution properties
of 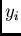 should be carefully checked.
should be carefully checked.




Next: Fallstudie: Kohlelagerstätte
Up: Simulation of an Unconditional
Previous: The ``Turning Bands'' Method
Contents
Rudolf Dutter
2003-03-13
![]() in
the form of a convolution product of a function
in
the form of a convolution product of a function ![]() and its transpose
and its transpose
![]() :
:



![/begin{displaymath}C^{(1)}(s)= /int^/infty_{- /infty} f(u) /times f(u+s)du=
/int^{a/2-s}_{-a/2} (12C_{o}/a^{3})[u(u+s)]du/ / / ./end{displaymath}](img1156.png)
![]()
![]() with distance
with distance ![]() uniformly distributed
random numbers
uniformly distributed
random numbers
![]() in the interval
in the interval ![]() .
The distance
.
The distance ![]() should be at least
should be at least ![]() . Then a realization of
. Then a realization of ![]() (the one-dimensional random function) is produced through linear
combination (moving average)
(the one-dimensional random function) is produced through linear
combination (moving average)
